What are the chances of a specific outcome occurring? That is the leading question of probabilistic thinking. It’s a mathematical concept that defines the field of statistics. But it applies to every field that includes some measure of uncertainty. It’s a great tool for decision-making and any type of risk management.
Probabilistic thinking helps you to better forecast the future. From this point onwards, the future is a collection of possible scenarios, but not all of them are equally likely to occur. Based on the information you have, you can assign probabilities to each potential outcome and bet on the most likely.
Examples
Prediction Markets
Prediction markets are a pure example of probabilistic thinking. It’s a market where people bet on specific outcomes to occur. For example, the question is “Who is the next UK Conservative leader?”. The question is bound by a timeframe and options. People then can bet on whatever option they like. The more confident people are in their predictions the higher they will bet. The market price for each option indicates what the crowd thinks the probability of the event is. In the end, the winners get cashed out.

Insurance
An insurance company relies on probabilistic thinking to not go broke. They underwrite different risks by assigning probabilities to possible scenarios.
For example, if you take up insurance on water damage on your house, you’ll pay a different premium based on the house’s location. In an area with regular floods, there is a much higher likelihood that your house is damaged and hence, the premium for the insurance will be higher.
The ideal insurance is priced in a way that it is still attractive for individuals, however, the insurance firm wins out over all individual insurances they’ve sold. If an insurance company gets this wrong, it might go bust as soon as an outsized event occurs that affects a lot of individuals. Or they continuously lose money on a policy that was underwritten with erroneous probabilities.
Value at Risk
Value at Risk (VaR) is a fundamental risk management tool when it comes to limiting a portfolio’s downside. It is widely used in financial and other industries. VaR defines the worst loss that is expected to happen with a certain confidence level under normal circumstances.
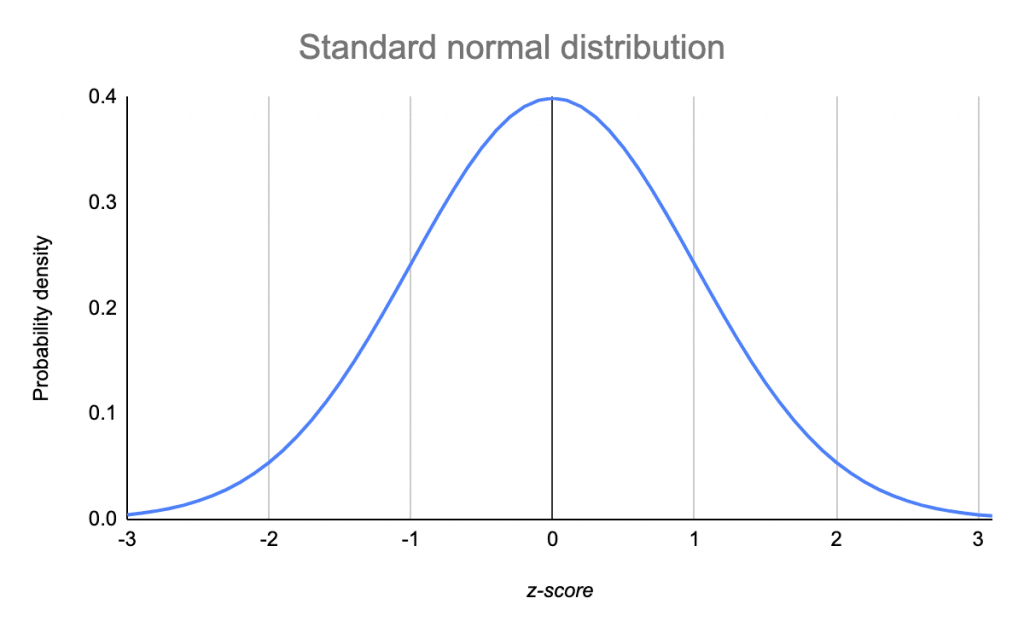
This is often done using probability theory. Let us assume an investor recorded daily price changes of a stock over the past 50 years. The price changes are evenly distributed around the mean. The X-Axis defines their respective size, while the Y-Axis describes the frequency of occurrence. Hence, the small profit and losses around point 0 occur often but are relatively small. The larger changes, which in turn occur more seldom, can be found in the respective tails.
If one believes that the past is a reliable predictor of the future, one would assume that future outcomes are equally distributed. Hence, the VAR measure could reliably be used to calculate the probability of default. For instance, a VaR measure of $100 million over a day with a confidence level of 95% means that the expected losses over a day will lie within two standard deviations of the mean. Hence, the expected losses do not exceed $100 million with a probability of 95%.
Thus, if a firm does not want to default with a probability of 95% in a day, it should have capital put aside of $100 million. The capital requirement increases both with a higher confidence level, because more extreme potential losses must be covered, as well as a longer time horizon, because more could happen and the probability for occurrences naturally increases.
Ultimately VaR determines at each confidence level, what the largest expected loss is. It defines the amount of capital that should be set aside to insure against default. VaR can be calculated for all the different investment positions and aggregated to an overall default measure. Of course, this is simplified, there are other aspects, such as intercorrelation of positions, that are considered for a more complete aggregate measure. However, the fundamental aspects stay the same and the metric is heavily dependent on the respective probability distribution.
Application
Thinking in bets
Most people naturally think in either absolutes or fuzzy terms. An event is often “impossible” or “always”, “sometimes” or “once in a while”. While this amount of precision is enough for small talk and polite conversation, it isn’t very useful in practice.
A much better way of thinking about the accuracy of our beliefs or the likelihood of future events is by assigning probabilities to them.
Forcing ourselves to express how sure we are of our beliefs brings to plain sight the probabilistic nature of those beliefs, that what we believe is almost never 100% or 0% accurate but, rather, somewhere in between. – Annie Duke
This has the additional benefit that it’s easier to change our beliefs because we feel less invested in them personally. It’s hard for our ego to admit we’ve been wrong. But with probabilities, it’s no longer a question of being right or wrong.
“I was 58% but now I’m 46%.” That doesn’t feel nearly as bad as “I thought I was right but now I’m wrong.” Our narrative of being a knowledgeable, educated, intelligent person who holds quality opinions isn’t compromised when we use new information to calibrate our beliefs, compared with having to make a full-on reversal. – Annie Duke
This practice of adjusting our probability estimates with new information is called Bayesian updating. At every point, you make up your mind based on the information you have. As soon as you learn something new that is significant to your belief, you should adjust it based on that new knowledge. This sounds very obvious and it is on the surface level. But as soon as you start thinking about how much you need to update your belief it gets complicated. It’s even harder to do psychologically. Focus on the principle and not the technicalities.
The superforecasters are a numerate bunch: many know about Bayes' theorem and could deploy it if they felt it was worth the trouble. But they rarely crunch the numbers so explicitly. What matters far more to the superforecasters than Bayes' theorem is Bayes' core insight of gradually getting closer to the truth by constantly updating in proportion to the weight of the evidence. — Philip Tetlock and Dan Gardner, Superforecasting
Predictably wrong
It isn’t natural for us to make probability calculations in our head. Imagine a human five thousand years ago, hearing a rustling in a nearby bush. Before she can calculate the probability of there being a lion based on past experience and information she got from her friends last night by the fire, she will get eaten. Her less thoughtful neighbor who always runs if he hears rustling in the bush will survive, both when there is a lion and when there isn’t.
Through this logic, humans developed countless heuristics that allow them to gauge risk quickly and make decisions. With the change of our environment we now have to make very different decisions however, and a lot of the heuristics are no longer useful and even predictably wrong.
You have to be aware of these biases when you’re practicing your probabilistic thinking:
Outcome bias: When you equate the outcome of your decision with the quality of your decision you’re falling prey to outcome bias. Since we’re dealing with probabilities here there is no certainty. You could have made all the right decisions and estimated all the probabilities correctly and in the end, just get dealt some bad cards. Don’t learn the wrong lesson!
Hindsight bias: It’s always easier to look back and criticize your mistakes. Looking back, it might seem like the outcome has been inevitable. However, you should always evaluate past decisions based on the context you’ve been in at the time and not on the information you’ve gained in the meantime. It always looks obvious in hindsight.
Correlation is not causation: Just because two metrics correlate, doesn’t mean that they impact each other. There is a whole website with ludicrous correlations. Let that be a warning.
When we work backward from results to figure out why those things happened, we are susceptible to a variety of cognitive traps, like assuming causation when there is only a correlation, or cherry-picking data to confirm the narrative we prefer. We will pound a lot of square pegs into round holes to maintain the illusion of a tight relationship between our outcomes and our decisions. – Annie Duke
Positioning rather than prediction
A Black Swan is an unpredictable, irregular, and large-scale event with severe consequences. The concept was coined in the book with the same name by Nassim Nicholas Taleb.
How can you use probabilistic thinking to deal with this? You can’t since these events are by definition unpredictable. The solution to the Black Swan problem is that although risk cannot be determined, fragility can be measured.
Fragility is characterized by negative asymmetry, i.e. there is more downside than upside from random events.
Antifragility is characterized by positive asymmetry, i.e. there is more upside than downside from random events.
All you need is the wisdom to not do things that hurt yourself (bet everything on one card for instance) and put yourself in a position to benefit from favorable outcomes when they occur.
Limitation
Nothing in life is certain. Everything is a question of probability. However, because reality is often too complex for us to comprehend there’s always the danger of wrong assumptions and missing variables. Keep in mind the cost of being wrong and don’t rely on probabilistic thinking completely. Hedge your bets and avoid risks that could make you go bust.
Encoding Image
🃏 Poker cards. Unlike chess, the game of poker is riddled with uncertainty and incomplete information. Every decision you make you must make is based on probability estimates. What is the chance of your opponent having the winning hand? How high is the probability of your opponent bluffing? Every step of the game the probabilities change. Every action provides new information. Because of that, poker is a great representation of probabilistic thinking in action.
Quotes
Skepticism is about approaching the world by asking why things might not be true rather than why they are true. – Annie Duke
Improving decision quality is about increasing our chances of good outcomes, not guaranteeing them. – Annie Duke
It ain’t what you don’t know that gets you into trouble. It’s what you know for sure that just ain’t so. – Mark Twain